Key-words
Composite materials, equivalent medium, multiscale approach, homogenization, relocation, thermal conduction, macroscopic and microscopic medium, alloys, heterogeneous medium.
Context / Goal
Composite materials are employed to lighten an internal combustion engine of a race car. Some parts, as the intake manifold (Figure 1), are made of weaved carbon fiber and a resin. Using this material, the intake manifold is both very light and very resistant.
However, this resistance depends on a good bond between the fibers and the resin matrix: when the engine is hot while cold air flows through the air intake, important variations of the temperature are locally observed. The goal of this study is to determine the maximum amplitude of the local thermal dilatation, which could be understood as the fiber delamination from the matrix.
SIMTEC's Achievements / Results
A direct modeling of thermal exchanges, which includes both the microscopic scale of the fibers and the macroscopic scale of the entire part, would require immense computing resources and a very long solving time: the coexistence of both scales makes it necessary to use a very fine mesh over a very large domain.
To tackle this issue accurately and efficiently, SIMTEC has developed a periodic homogenization method, allowing to solve the macroscopic problem while still accounting for the microstructure of the material.
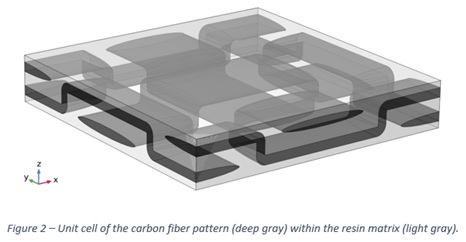
The method is based on the definition of a unit cell of the composite material (Figure 2). Computations determined by the method on this unit cell allow to obtain a homogenized conductivity of the heterogeneous material. Here, this conductivity depends on the axis:
The temperature in the whole intake manifold can then be computed accurately (Figure 3).
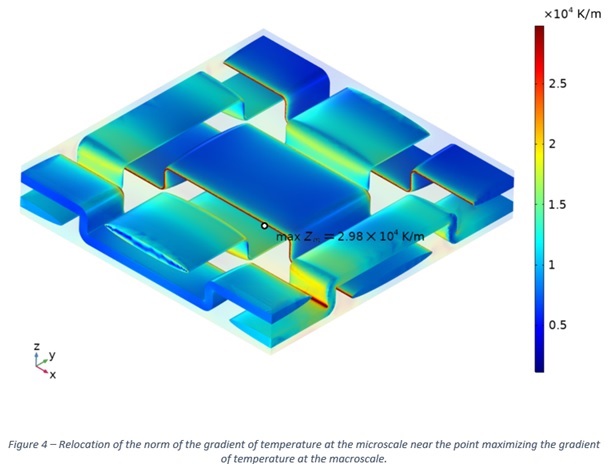
This computation also makes it possible to determine the macroscopic gradient of temperature within the whole intake manifold, , and its maximal value attained at the interface between the part and the engine. However, this value is far from the amplitude of the gradient at the microscopic scale (1.02e4 K/m versus 2.98e4 K/m).
The periodic homogenization method allows for reconstructing accurately the temperature field and its gradient at the microscale, allowing to deduce the dilatation of the materials at the fiber/matrix interface (Figure 4). Then, at the microscale, there are locations on the fiber/matrix interface whose extremal value of the gradient of temperature is three times more than the macroscopic gradient.
Thus, SIMTEC’s study allows to consider the material at the macroscale, while taking into account its microstructure, in order to quantify the thermal dilatation at the fiber/matrix interface of a composite material. In a second step, such an approach allows for optimizing designs by minimizing the weight while ensuring their integrity.
Depending on the application, other microstructures can be considered by the method, as the honeycombs (Figure 5), or pseudo-periodical structures (Figure 6).